Spokojnie! Mimo, że Polaków ogarnął szał rozliczeń podatkowych (tzw. pit’olenie), ten artykuł nie traktuje o podatku od zysków kapitałowych. Jest to kawał inżynierskiej wiedzy, jak zawsze na SOLIDMANII.
Belka to, w ujęciu symulacji numerycznych MES, element liniowy stawiający opór siłom osiowym (rozciągającym i ściskającym) i momentowi obrotowemu oraz siłom tnącym i momentom zginającym.
Dwa pierwsze odnoszą się do osi wzdłużnej belki. Dwa ostatnie odnoszą się do przekroju prostopadłego do osi wzdłużnej.
Zrozumieniu tych wszystkich składowych służy układ, indywidualny dla każdej belki, który pokazuje Kierunki belki (rys. 1).
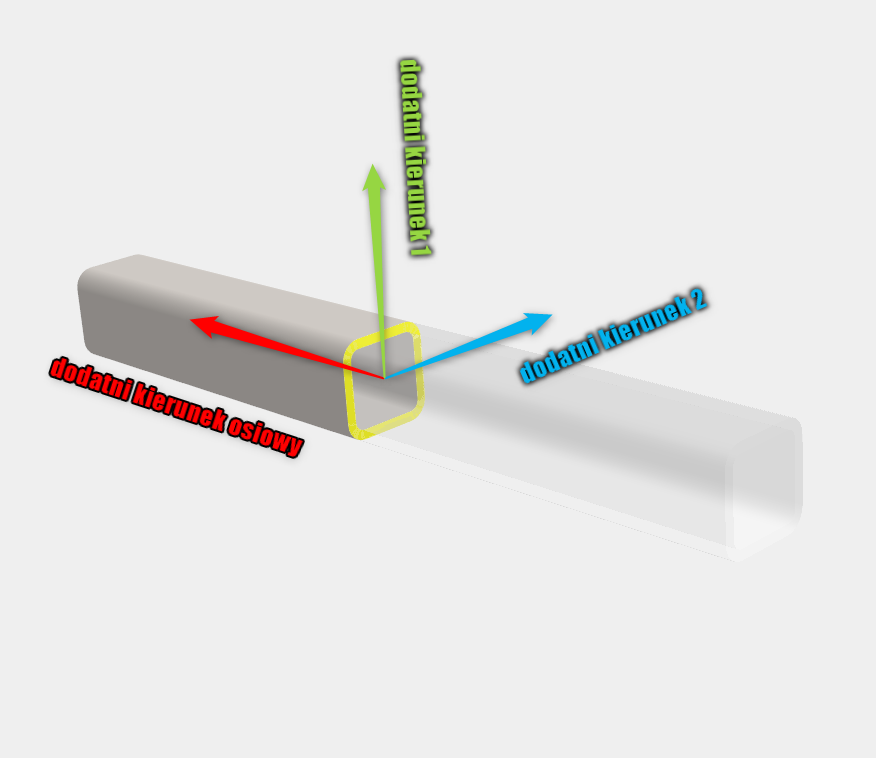
Rys. 1. Kierunki belki
Symbolika jest tu zawsze stała i jasno określona. Kierunek osiowy (oznaczony kolorem czerwonym) pozwoli odnieść się do obciążeń siłami osiowymi i momentem obrotowym. Dwa kierunku prostopadłe do osi wzdłużnej (oznaczone kolorami zielonym i niebieskim) pozwolą odnieść się do obciążeń siłą tnącą i momentem zginającym. Co ważne, groty strzałek wskazywać będą zawsze kierunki dodatnie. Tak więc znak będzie odnosić się do tego układu, a nie ogólnie przyjętych zasad określania znaków reakcji i utwierdzenia. Kierunki 1 i 2 będą również pomocne w określeniu, na której płaszczyźnie utworzony zostanie wykres belki, w zależności od kierunku działania sił czy osi dla momentów.
Mając informacje o Kierunkach belki, oraz oczywiście o schemacie obciążeń, możemy precyzyjnie wykreślić rozkłady sił i momentów wzdłuż długości belki (rys 2).
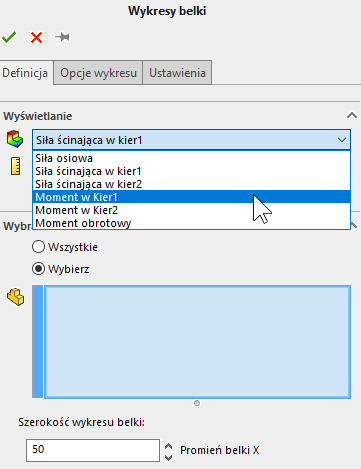
Rys. 2. Wstawianie Wykresu belki
Pracując na modelu zbudowanym z wielu belek możemy wskazać te, dla których wykres ma zostać wygenerowany. Dla lepszej przejrzystości wykresów (wysokość słupków) dostosować należy parametr szerokości wykresu belki.

Rys. 3. Przykładowe wykresy
Kolejno tworzone wykresy wstawiane są do folderu Wyniki w drzewie badania (rys. 3).
Belka jednostronnie utwierdzona obciążona jedną siłą czynną
Rozpatrzmy belkę kwadratową o długości 1,3 m obciążoną siłą o wartości 1000 N skupioną w punkcie oddalonym o 1 m od utwierdzenia:
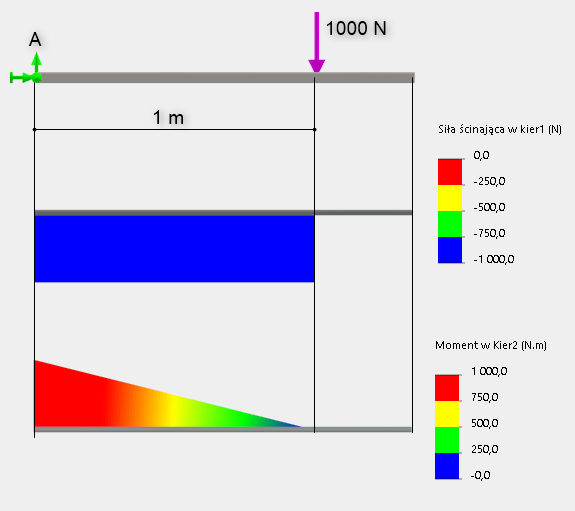
Rys. 4. Schemat obciążenia siłą oraz wykresy siły tnącej i momentu zginającego
Sprawdźmy!
Siła tnąca w utwierdzeniu A:
![]()
Moment zginający w utwierdzeniu A:
![]()
<uzgodnienie znaku +/- jest skorelowane z Kierunkiem belki i został pominięty w obliczeniach analitycznych>
Belka jednostronnie utwierdzona obciążona jednym momentem czynnym
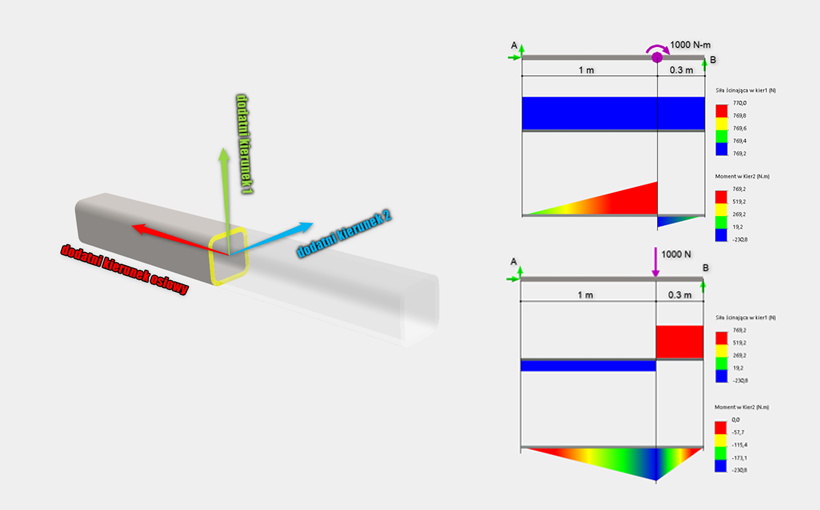
Rozpatrzmy belkę kwadratową o długości 1,3 m obciążoną momentem o wartości 1000 N-m przyłożony w punkcie oddalonym o 1 m od utwierdzenia:
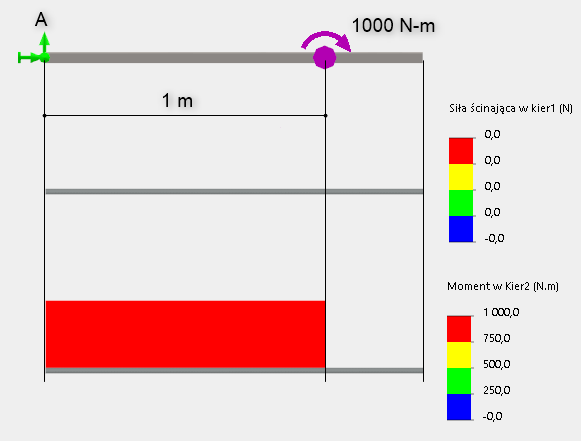
Rys. 5. Schemat obciążenia momentem oraz wykresy siły tnącej i momentu zginającego
Sprawdźmy!
Siła tnąca w utwierdzeniu A:
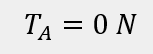
Moment zginający w utwierdzeniu A:
![]()
<uzgodnienie znaku +/- jest skorelowane z Kierunkiem belki i został pominięty w obliczeniach analitycznych>
Belka swobodnie podparta obciążona jedną siłą czynną
Rozpatrzmy belkę kwadratową o długości 1,3 m obciążoną siłą o wartości 1000 N skupioną w punkcie oddalonym o 1 m od podpory nieprzesuwnej z przegubem:
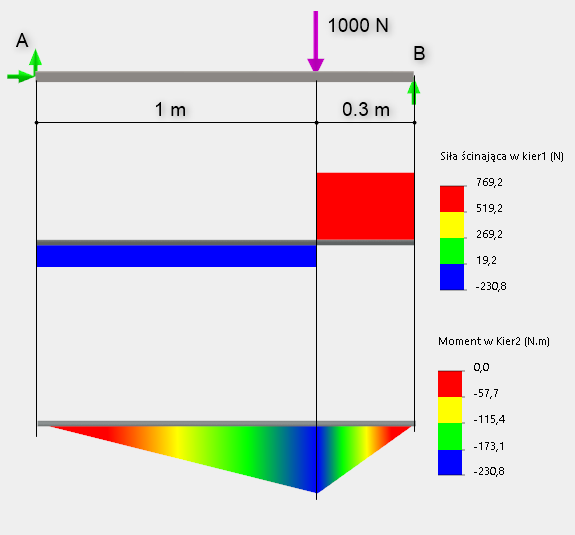
Rys. 6. Schemat obciążenia siłą oraz wykresy siły tnącej i momentu zginającego
Sprawdźmy!
Siła tnąca w podporze A:

Siła tnąca w podporze B:
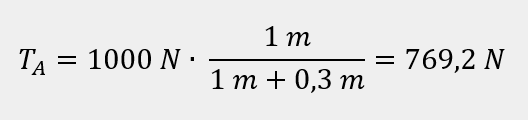
Moment zginający w punkcie przyłożenia siły po stronie podpór A i B:
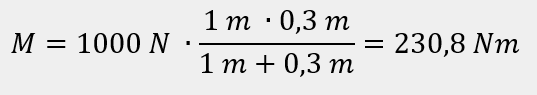
<uzgodnienie znaku +/- jest skorelowane z Kierunkiem belki i został pominięty w obliczeniach analitycznych>
Belka swobodnie podparta obciążona jednym momentem czynnym
Rozpatrzmy belkę kwadratową o długości 1,3 m obciążoną momentem o wartości 1000 N-m przyłożonym w punkcie oddalonym o 1 m od podpory nieprzesuwnej z przegubem:
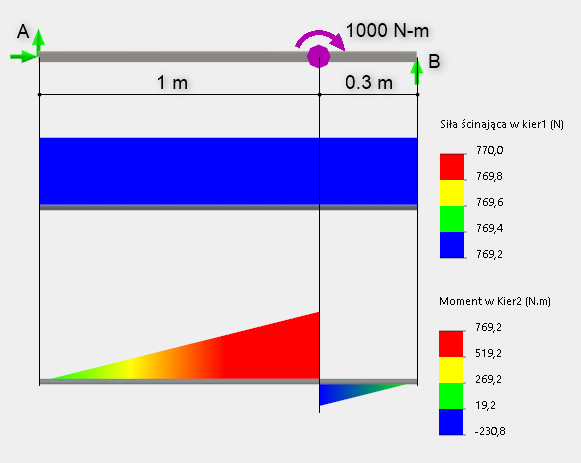
Rys. 7. Schemat obciążenia momentem oraz wykresy siły tnącej i momentu zginającego
Sprawdźmy!
Siła tnąca w punkcie przyłożenia momentu :
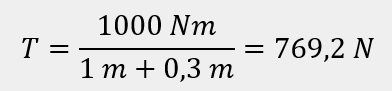
Moment zginający w punkcie od strony podpory A:
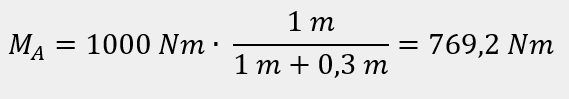
Moment zginający w punkcie od strony podpory B:
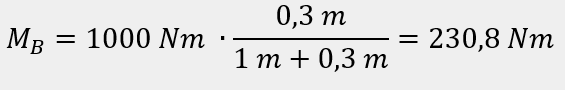
<uzgodnienie znaku +/- jest skorelowane z Kierunkiem belki i został pominięty w obliczeniach analitycznych>
Informacje dodatkowe
Kluczowa, zwłaszcza przy wykreślaniu momentu obrotowego, jest charakterystyka przekroju belki. Model dyskretny nie posiada tych informacji, gdyż jak wspomniano wcześniej, belka jest elementem liniowym. Niemniej jednak w ramach Edycji definicji informacje takie są zawarte dla każdej belki.

Rys. 8. Parametry przekroju poprzecznego belki
Właściwości te wyznaczane są automatycznie na podstawie geometrii CAD (rys. 8). Dane te można jednak swobodnie modyfikować, bez konieczności wprowadzania zmian w modelu geometrycznym.
Podsumowanie
Stosowanie elementów belkowych (liniowych) w modelu dyskretnym do obliczeń numerycznych, pozwala na tworzenie wykresów obrazujących rozkład sił i momentów wzdłuż długości belki. Wykresy te w sposób graficzny przedstawiają charakter obciążeń wewnętrznych, jakie wywołują obciążenia działające na belkę. Stanowi to całkiem niezłą alternatywę dla obliczeń analitycznych, zwłaszcza w przypadku skomplikowanych ram czy kratownic.