Wstęp
Powszechnie wiadomo, że symulacje numeryczne są bardzo cennym narzędziem w projektowaniu nowego produktu. Pozwalają na wirtualną walidację produktu, co znacząco zmniejsza liczbę wymaganych fizycznych prototypów oraz pozwalają na adaptację istniejących rozwiązań do specyficznych wymagań klientów. Jako standardową procedurę stosujemy symulacje numeryczne do analizy szeroko rozumianej mechanicznej, mechaniki płynów, transportu ciepła i masy oraz symulacji zjawisk elektromagnetycznych. Szerokie spektrum analizowanych procesów, wymaga zastosowania różnych metod numerycznych, co przekłada się na konieczność skorzystania z różnych programów. Użytkownicy oprogramowania SOLIDWORKS mają dostęp do trzech różnych rozwiązań symulacyjnych: SOLIDWORKS Simulation, SOLIDWORKS Flow Simulation oraz SOLIDWORKS Plastics. Każde z nich dedykowane jest do konkretnych typów analiz:
- Simulation – obliczenia mechaniczne;
- Flow Simulation – analiza przepływów cieczy i gazów;
- Plastics – symulacji procesów wtrysku tworzyw sztucznych.
Jednak jest pewien obszar, wspólny dla programów SOLIDWORKS Simulation i SOLIDWORKS Flow Simulation – analiza termiczna. Ponieważ oba wspomniane programy opierają się na różnych metodach numerycznych, wielu użytkowników może ciekawić, jak różnice w tych metodach wpływają na wyniki. W niniejszym artykule chciałbym krótko omówić te metody oraz różnice między nimi, a także pokazać ich zastosowanie w analizie termicznej na tych samych, wybranych przykładach.
SOLIDWORKS Simulation – FEA
SOLIDWORKS Simulation jest oprogramowaniem dedykowanym do analizy numerycznej z wykorzystaniem elementów skończonych (ang. Finite Element Analysis, FEA). Oprogramowanie korzysta z najbardziej znanej i powszechnej metody numerycznej – metody elementów skończonych (ang. Finite Element Method, FEM), która służy do dyskretyzacji domeny obliczeniowej. Sprowadza się ona do podzielenia obiektu który analizujemy na mniejsze skończone elementy (ang. finite element), które opisane są przez funkcje bazowe. Funkcje bazowe pozwalają na interpolację poszukiwanej funkcji, przez co użytkownik ma możliwość wykonania obliczeń w obszarach o skomplikowanych kształtach, dla których nie ma rozwiązań analitycznych. Istnieją różne rodzaje elementów: jednowymiarowe, dwuwymiarowe (powierzchniowe), trójwymiarowe (bryłowe), które mogą mieć różną geometrię (np. czworościenne i sześcienne elementy 3D) oraz różną liczbę węzłów przypadających na jeden element (rząd elementu). W przypadku oprogramowania SOLIDWORKS Simulation, użytkownicy maja dostęp do elementów trójkątnych 2D i czworościennych 3D, pierwszego i drugiego rzędu (siatka roboczej i wysokiej jakości). Przykłady siatek 2D i 3D generowanych w SOLIDWORKS Simulation przedstawiono na Rys. 1.
 |
 |
Rys. 1 Przykłady siatki wysokiej jakości: czworościennej 3D (lewo) oraz trójkątnej 2D (prawo).
SOLIDWORKS Flow Simulation – CFD
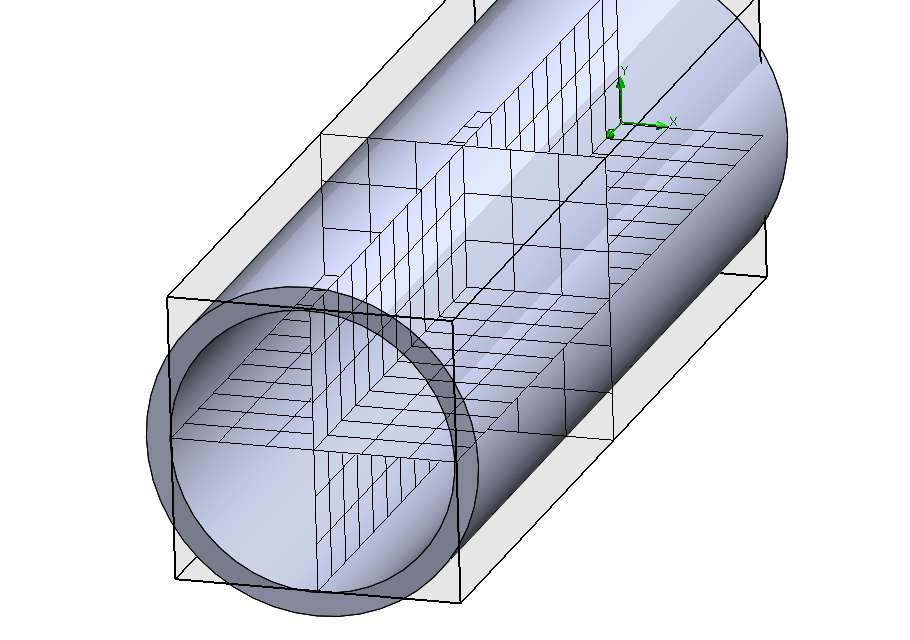
SOLIDWORKS Flow Simulation jest oprogramowaniem dedykowanym do komputerowej dynamiki płynów (ang. Computational Fluid Dynamics, CFD). W przeciwieństwie do FEA, nazwa CFD odnosi się do typu analizy, a nie konkretnej metody numerycznej. Obliczenia CFD można wykonywać z wykorzystaniem wielu metod numerycznych takich jak m.in. metoda różnic skończonych (FDM), metoda sieciowa Boltzmanna (LBM), metoda elementów skończonych (FEM) oraz wiele innych. Jednak najczęściej stosowana metoda numeryczną jest metoda objętości skończonej (Finite Volume Method, FVM), z której korzysta oprogramowanie SOLIDWORKS Flow Simulation. W metodzie objętości skończonej, całki objętościowe w równaniach różniczkowych cząstkowych, zawierające człon dyferencyjny są przekształcane w całki powierzchniowe z wykorzystaniem twierdzenia Ostrogradskiego-Gaussa. Następnie człony te uwzględniane są jako strumienie do powierzchni każdej ze skończonych objętości. Ze względu na zastosowanie metody FVM w dynamice płynów, dyskretyzacja przestrzeni jest inna niż w przypadku metody FEM, gdzie objętość analizowanego obiektu jest podzielona na skończone elementy (czworościany w przypadku SOLIDWORKS Simulation). W SOLIDWORKS Flow Simulation (FVM) możliwa jest analiza wewnętrzna (siatka tworzona jest w pustych przestrzeniach bryły), zewnętrzna (siatka tworzona jest na zewnątrz bryły) oraz wariant mieszany, który tworzy również siatkę wewnątrz bryły tak, aby możliwe było wykonanie obliczeń np. transportu ciepła w objętości bryły. Konsekwencją zasady działania metody FVM oraz typów analiz (wewnętrzna i zewnętrzna) siatka obliczeniowa, którą stosujemy w tej metodzie jest zbudowana z prostopadłościanów. Przykłady siatek i domen obliczeniowych dla analiz wewnętrznych i zewnętrznych zaprezentowano na Rys. 2. Dokładny opis siatki w programie SOLIDWORKS Flow Simulation przedstawiliśmy w innym artykule.
 |
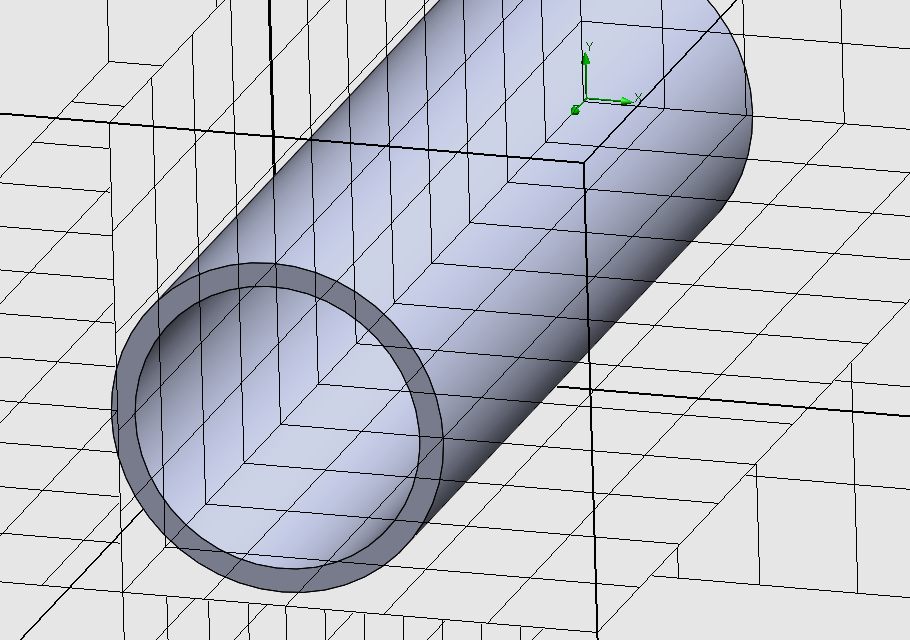 |
Rys. 2 Przykłady siatki (3 przecinające się powierzchnie) oraz domeny obliczeniowej (czarny prostopadłościan) w symulacji przepływu: wewnętrznego (lewo) oraz zewnętrznego (prawo).
Dlaczego FEM dla ciał stałych a FVM dla cieczy?
Mając ogólne pojęcie o różnicach między metodami FEM i FVM, pozostaje odpowiedzieć na pytanie dlaczego metoda FEM jest stosowana do symulacji ciał stałych, a metoda FVM do symulacji cieczy. Jest to oczywiście konsekwencja równań stosowanych do opisu przemieszczenia.
W przypadku analizy płynów, do opisu przemieszczenia stosujemy równania Naviera-Stokesa, które zawierają nieliniowy człon konwekcyjny, co czyni problem niesymetrycznym. W konsekwencji metoda FEM bazująca na formule Galerkina zawodzi, jeśli nie ma członu stabilizacyjnego. Z drugiej strony metoda FVM bazująca na prawie zachowania ma możliwość poradzenia sobie z niesymetrycznością bez wprowadzania członu stabilizacyjnego. Jest to główny powód dla którego symulacje cieczy przeprowadzane są głównie z wykorzystaniem metody FVM. W konsekwencji w niektórych opracowaniach pojęcia CFD i FVM są używane zamiennie, co jest zdecydowanie zbyt dużym uproszczeniem, ale jednak oddającym zdecydowaną popularność metody FVM w symulacjach płynów.
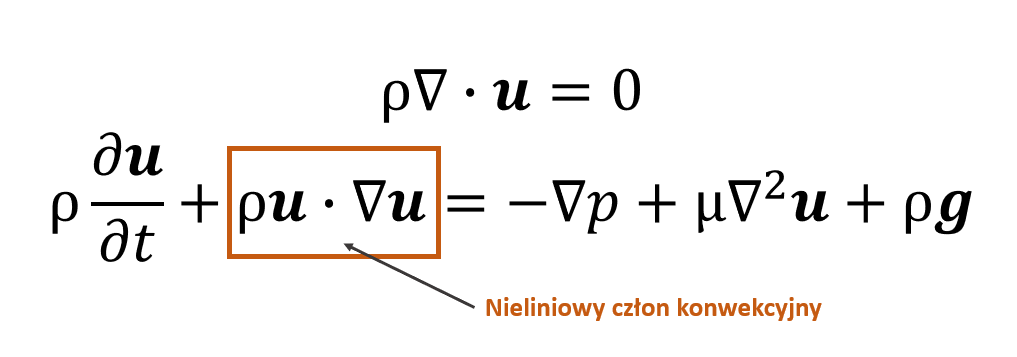
Rys. 3 Równania Naviera-Stokesa.
Metoda FEM jest z kolei stosowana z bardzo dużym powodzeniem w zagadnieniach mechaniki ciał stałych, gdzie równania są symetryczne (samosprzężone eliptycznie), przez co standardowa metoda FEM z wykorzystaniem formuły Galerkina staje się idealnym rozwiązaniem takiej klasy zagadnień. Metoda FEM jest tak popularna i stosowana z sukcesem, że jest synonimem analizy strukturalnej.
Mechanizmy wymiany ciepła
Po zapoznaniu się z metodami FEM i FVM, różnicami między nimi i ich typowym zastosowaniem pora zapoznać się z obszarem dla nich wspólnym – transportem ciepła. Symulacje transportu ciepła sprowadzają się do rozwiązania równania bilansu energii:
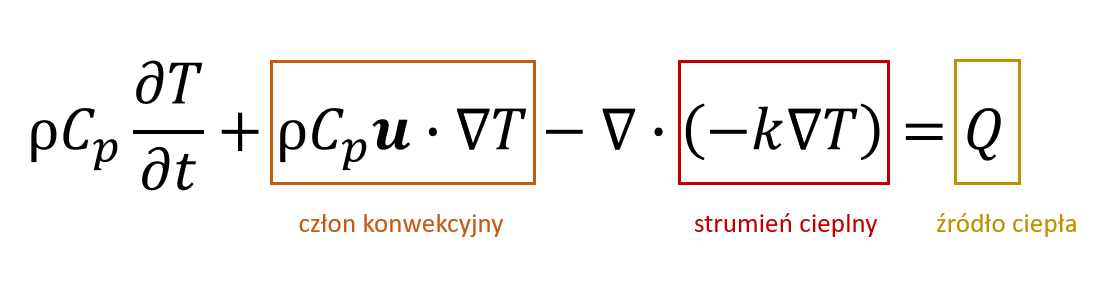
Jak można zauważyć, równanie bilansu energii zawiera człon konwekcyjny jeśli rozpatrujemy transport ciepła w płynie. W przypadku transportu w ciele stałym, człon ten jest pomijany. Z założenia wiemy, że niezależnie od ośrodka, metody FVM i FEM powinny pozwolić na otrzymanie rozwiązania w symulacji transportu ciepła. Spodziewamy się, że w przypadku transportu w płynie, lepiej byłoby skorzystać z metody FVM. Ale zanim przejdziemy do bezpośredniego porównania metod, musimy krótko omówić fizykę stojącą za transportem ciepła – mechanizmy wymiany ciepła. Wyróżniamy wśród nich:
- Przewodzenie – mechanizm dominujący w ciałach stałych, polegający na przekazywaniu energii przez zderzenia molekuł, bez makroskopowego ruchu materii. Parametrem definiującym efektywność transportu ciepła jest współczynnik przewodzenia ciepła, k [W/mK], który występuje w równaniu bilansu energii (a dokładniej w wyrażeniu na strumień cieplny).
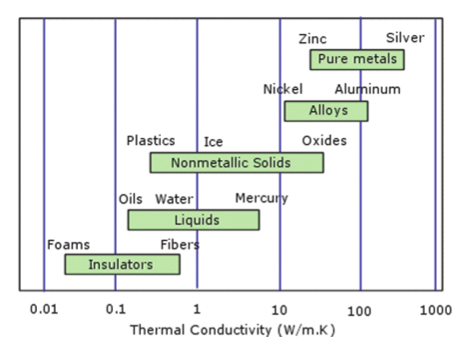
Rys. 4 Zakres wartości współczynnika przewodzenia ciepła dla wybranych ciał stałych i cieczy.
- Konwekcję – mechanizm dominujący w płynach, wynikający z przemieszczenia się masy płynu (cieczy lub gazu). W przypadku konwekcji możemy wymienić jej dwa rodzaje:
-
- Naturalna (swobodna) – ruch płynu wywołany jest różnicą gęstości płynu wynikającą z różnicy temperatur;
- Wymuszona – ruch płynu wywołany jest czynnikami zewnętrznymi (np. pompa, wentylator).
-
Parametrem, który definiuje efektywność wymiany ciepła na drodze konwekcji, jest współczynnik wnikania ciepła, h [W/m2K]. Uwzględniamy go w symulacji jako warunek brzegowy na powierzchni między ciałem stałym a płynem:
gdzie: TS – temperatura powierzchni, TF – temperatura płynu. Przykładowe wartości współczynnika wymiany ciepła przedstawiono w poniższej tabeli:
| Płyn | Współczynnik wnikania ciepła, h (W/m2K) |
| Powietrze (naturalna konwekcja) | 5 – 25 |
| Powietrze (wymuszona konwekcja) | 20 – 300 |
| Olej (wymuszona konwekcja) | 60 – 1800 |
| Woda (wymuszona konwekcja) | 300 – 6000 |
| Woda (wrzenie) | 3000 – 60 000 |
| Para wodna (kondensacja) | 6000 – 120 000 |
- Promieniowanie – mechanizm dominujący w wysokich temperaturach, polega na przenoszeniu energii poprzez promieniowanie elektromagnetyczne. Nie wymaga obecności ośrodka pomiędzy ciałami, między którymi ciepło jest wymieniane – może zachodzić w próżni. Parametrem opisującym efektywność tego mechanizmu wymiany ciepła jest emisyjność powierzchni, ε, która przyjmuje wartości w zakresie od 0 (doskonałe odbicie) do 1 (pełne pochłanianie promieniowania). W symulacji promieniowanie uwzględniamy jako warunek brzegowy dany wzorem:
gdzie: σ – stała Stefana-Boltzmanna, TS – temperatura obiektu, TA –temperatura otoczenia.
Przeprowadzając analizy termiczne, musimy dysponować odpowiednimi parametrami materiałowymi. W każdej analizie niezbędna będzie znajomość współczynnika przewodzenia ciepła (k), natomiast współczynnik wnikania ciepła (h) oraz emisyjność powierzchni (ε) wymagane będą tylko w analizach uwzględniających odpowiednio konwekcję i/lub promieniowanie. Jednak w równaniu bilansu energii, można zauważyć dwa dodatkowe parametry: gęstość (ρ) oraz pojemność cieplną (CP). Parametry te nie zależą od mechanizmu wymiany ciepła, a od stanu układu. Kiedy rozpatrujemy ewolucję układu – rozważamy sposób w jaki układ zmienia się w czasie – wtedy konieczne będzie zdefiniowanie tych parametrów, aby symulować zmiany temperatury w czasie. W przypadku rozpatrywania zagadnień stacjonarnych, gęstość i pojemość cieplna nie są wymagane.
W dalszej części artykułu przedstawię zastosowania metod FEM i FVM (a więc programów SOLIDWORKS Simulation oraz Flow Simulation) do analizy różnych mechanizmów transportu ciepła na wybranych identycznych przykładach. Pomimo teoretycznej możliwości zastosowania metody FEM do symulacji przepływu płynu, program SOLIDWORKS Simulation nie wspiera takiej funkcjonalności. W konsekwencji analizowane przykłady nie będą zawierać symulacji transportu płynu.
Analiza przypadku – przewodzenie stacjonarne
W pierwszym przypadku skupimy się na samym procesie przewodzenia. Zrealizujemy to na prostym przypadku tygla, w którego środku został umieszczony ciekły metal (1550 oC), a ściany zewnętrzne są połączone z układem chłodzącym (300 oC). Ponieważ interesuje nas rozkład temperatury w ściankach tygla, objętość metalu wykluczymy z analizy. Możemy taki układ opisać za pomocą stałych wartości temperatury jako warunków brzegowych:
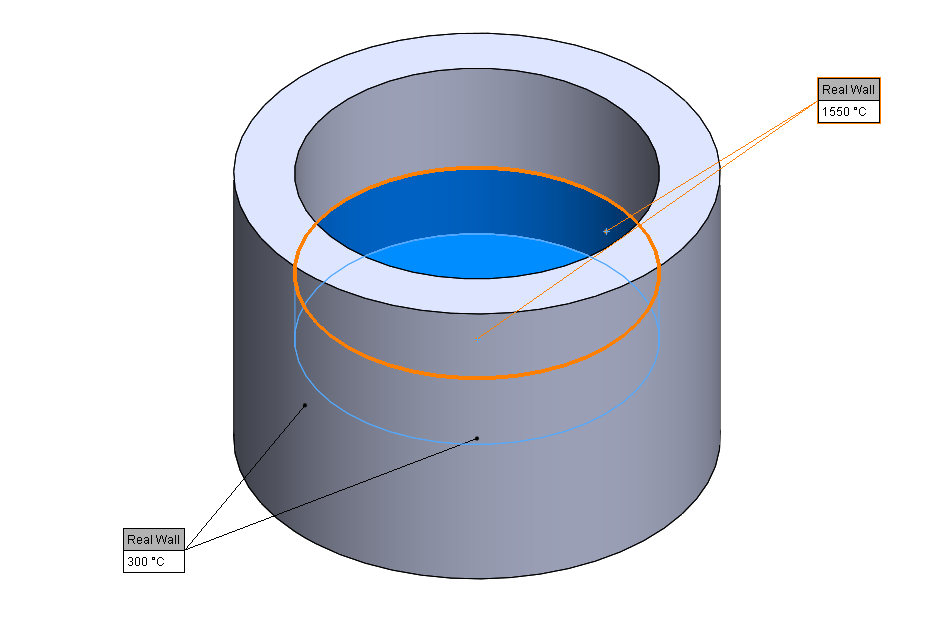
Rys. 5 Warunki brzegowe zastosowane w symulacji przewodzenia ciepła w ścianach tygla.
W obydwu symulacjach założono, że tygiel jest wykonany z przewodzącego materiału ogniotrwałego o współczynniku przewodzenia ciepła wynoszącym 30 W/mK. Ze względu na stacjonarny charakter symulacji, pojemność cieplna oraz gęstość teoretycznie nie są wymagane. Jednak w praktyce korzystając z programu SOLIDWORKS Flow Simulation, użytkownik musi podać te parametry, ponieważ wszystkie symulacje CFD są liczone jako procesy ewolucyjne, a dopiero po osiągnięciu zbieżności wyniki odpowiadają stanowi stacjonarnemu.
Definiowanie analizy w obydwu programach jest bardzo proste i intuicyjne – należy zdefiniować materiał oraz dwa warunki brzegowe:
– Obciążenia termiczne>Temperatura (Simulation)
– Boundary Conditions>Real Wall (Flow Simulation).
Ponieważ typ oraz sposób generowania siatki w obu programach jest kompletnie inny, praktycznie nie jest możliwe wykonanie siatek o identycznych parametrach. Parametry wykorzystanych siatek oraz czas obliczeń przedstawiono w tabeli poniżej:
| FEM | FVM | |
| Liczba elementów | 68 248 | – |
| Liczba stopni swobody | 85 083 | – |
| Liczba komórek | – | 43 440 |
| Czas obliczeń | 4 s | 6 s |
Można zauważyć, że pomimo mniejszej ilości komórek, czas obliczeń rozwiązania z wykorzystaniem metody FVM, jest dłuższy. Jednak ze względu na stosunkowo prosty przykład, czasy obliczeń są bardzo krótkie, a w konsekwencji również różnice między nimi. Otrzymane wyniki w postaci rozkładu temperatury przedstawiono na rysunkach poniżej:
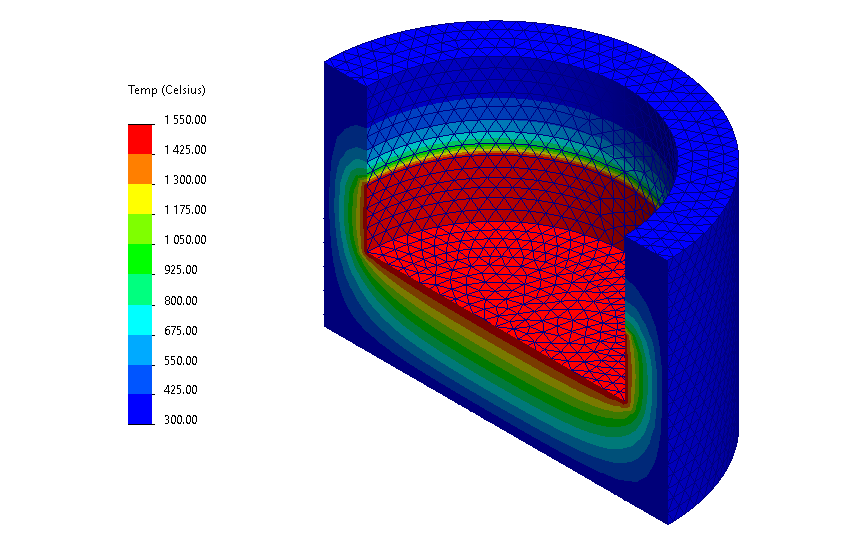 |
 |
Rys. 6 Rozkład temperatury w tyglu wyznaczony za pomocą: FEM (lewo) oraz FVM (prawo).
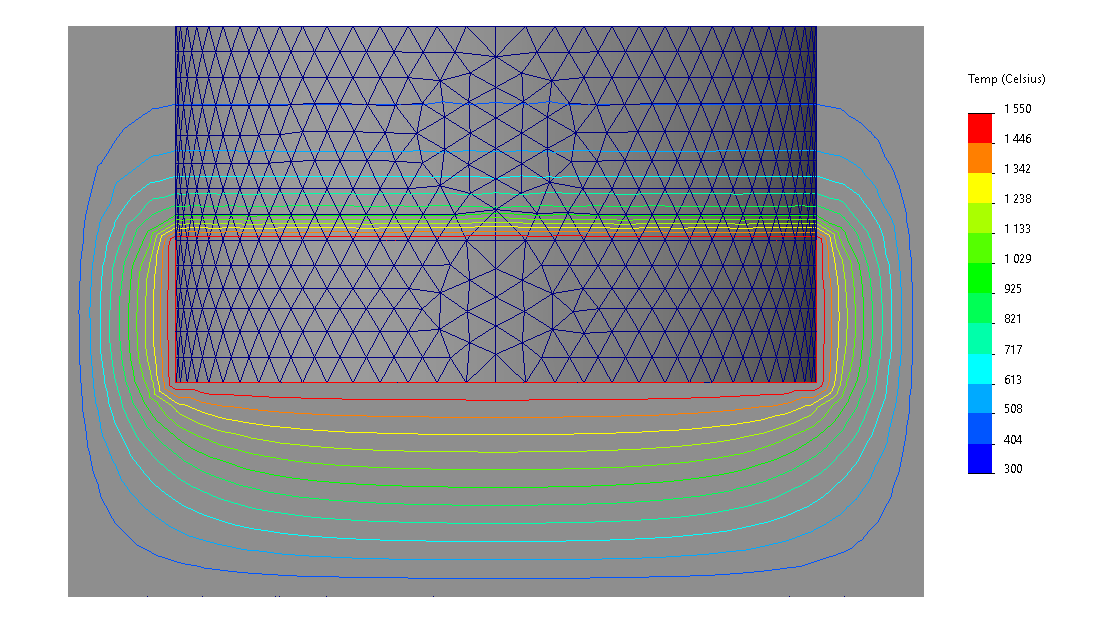 |
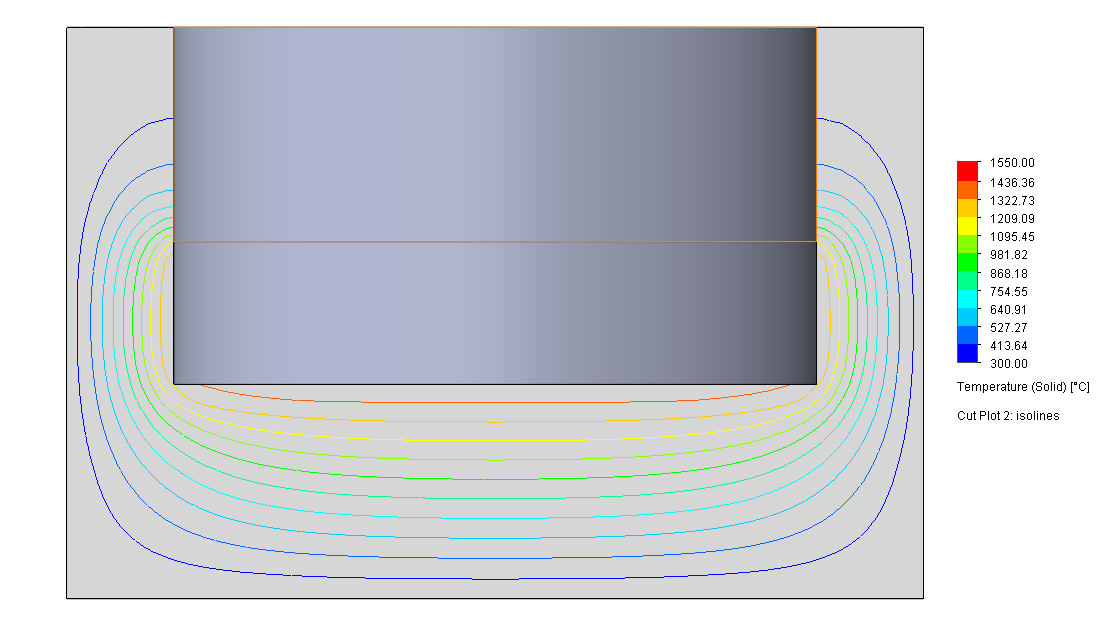 |
Rys. 7 Rozkład izoterm wyznaczony za pomocą: FEM (lewo) oraz FVM (prawo).
Na podstawie powyższych wykresów, można stwierdzić, że niezależnie od wybranej metody obliczeniowej, wyznaczone rozkłady temperatur w tyglu są takie same. Jedyna różnica między metodami FEM i FVM to czas obliczeń. W przypadku analizy procesu przewodzenia ciepła, metoda FVM nawet przy mniejszej ilości komórek wymaga dłuższego czasu obliczeń niż metoda FEM.
Analiza przypadku – przewodzenie i konwekcja w stanie nieustalonym
W drugim przypadku przeanalizujemy proces wymiany ciepła na drodze przewodzenia i konwekcji. Proces będzie zależał od czasu, czyli będzie w stanie nieustalonym. Celem analizy będzie złożenie składające się z ceramicznego mikroprocesora, miedzianego radiatora oraz trzech miedzianych złączy. Źródłem ciepła jest mikroprocesor, generujący moc cieplną wynoszącą 25 W. Wygenerowane ciepło transportowane jest do radiatora i oddawane do otoczenia (27 oC) na drodze konwekcji. Ze względu na dwa różne materiały (ceramikę i miedź), dwa różne współczynniki konwekcji muszą zostać uwzględnione. Złącza miedziane są izolowane. Dodatkowo zakładamy, że mikroprocesor połączony jest z radiatorem za pomocą 25 μm warstwy przewodzącego kleju, co wprowadza lokalna oporność termiczna. Dane wykorzystane w symulacji zestawiono w poniższej tabeli:
| Ceramika | Miedź | |
| Współczynnik przewodzenia ciepła [W/mK] | 1.495 | 390 |
| Pojemność cieplna [J/kgK] | 2300 | 390 |
| Gęstość [kg/m3] | 877.96 | 8900 |
| Współczynnik wnikania ciepła [W/m2K] | 100 | 250 |
| Oporność cieplna kleju [Km2/W] | 2.86 ∙ 10-6 | |
Geometrię złożenia mikroprocesora zaprezentowano na poniższym rysunku. Mikroprocesor, który jest objętościowym źródłem ciepła zaznaczono na niebiesko. Na zielono zaznaczono wierzchołek miedzianego złącza, który wykorzystano jako lokalną sondę do zobrazowania zmian temperatury w czasie. Obliczenia wykonano w zakresie od 0 do 300 s, z krokiem czasowym 10 s.
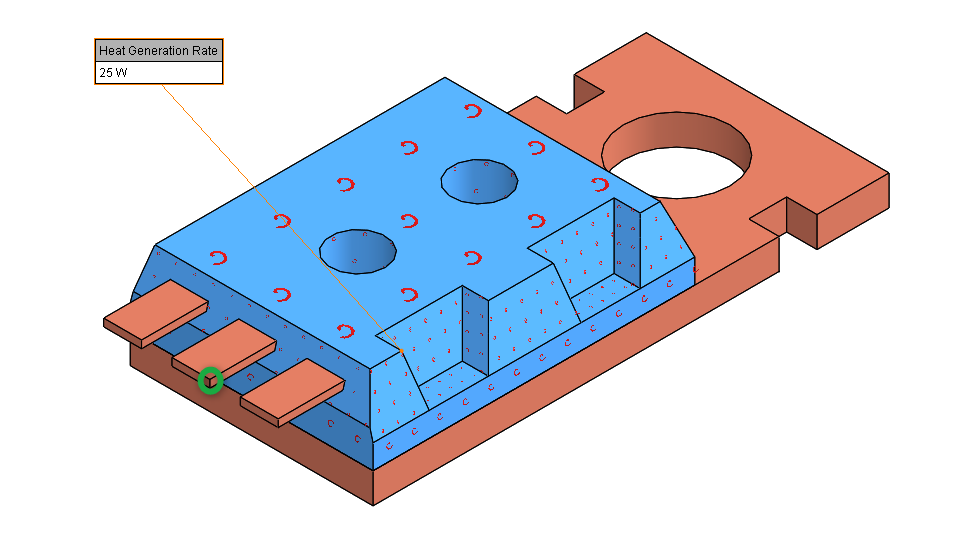
Rys. 8 Model CAD złożenia mikroprocesora z zaznaczonym źródłem ciepła (niebieski) oraz punktem pomiaru temperatury (zielony okrąg).
Podobnie jak w przypadku samego przewodzenia, porównano wykorzystane siatki oraz czas obliczeń. Informacje te zestawiono w poniższej tabeli:
| FEM | FVM | |
| Liczba elementów | 10 954 | – |
| Liczba stopni swobody | 18 453 | – |
| Liczba komórek | – | 25 034 |
| Czas obliczeń (ewolucyjny) | 58 s | 4 s |
| Czas obliczeń (stacjonarny) | 2 s | 3 s |
W przypadku ewolucyjnego procesu łączącego przewodzenie z konwekcją, pomimo, że siatka w metodzie FV, składa się z ponad 2 razy większej liczby komórek niż występuje elementów w siatce FEM, czas obliczeń jest znacząco krótszy (4s) niż w przypadku metody FEM (58s). Warto jednak zaznaczyć, że w porównaniu do pierwszego przypadku, nie tylko wprowadziliśmy nowy mechanizm transportu ciepła (konwekcję), ale również wprowadziliśmy obliczenia w funkcji czasu. Aby sprawdzić, który z tych czynników odpowiada za tak dużą różnicę w czasie obliczeń z wykorzystaniem FEM i FVM, wykonano obliczenia stacjonarne. W tym przypadku czas obliczeń był zbliżony – odpowiednio 2 s dla FEM i 3 s dla FVM. Oznacza to, że zastosowanie metody FVM jest zdecydowanie bardziej wydajne w analizie problemów w stanie nieustalonym.
Wyniki analizy w postaci rozkładu temperatury dla ostatniego kroku czasowego (300s) przedstawiono na (Rys. 9). Porównując wyniki można zauważyć, że są one zasadniczo identyczne. Widać również, że siatka zastosowana w metodzie FEM, jest zdecydowanie bardziej zgrubna niż zastosowana w metodzie FVM.
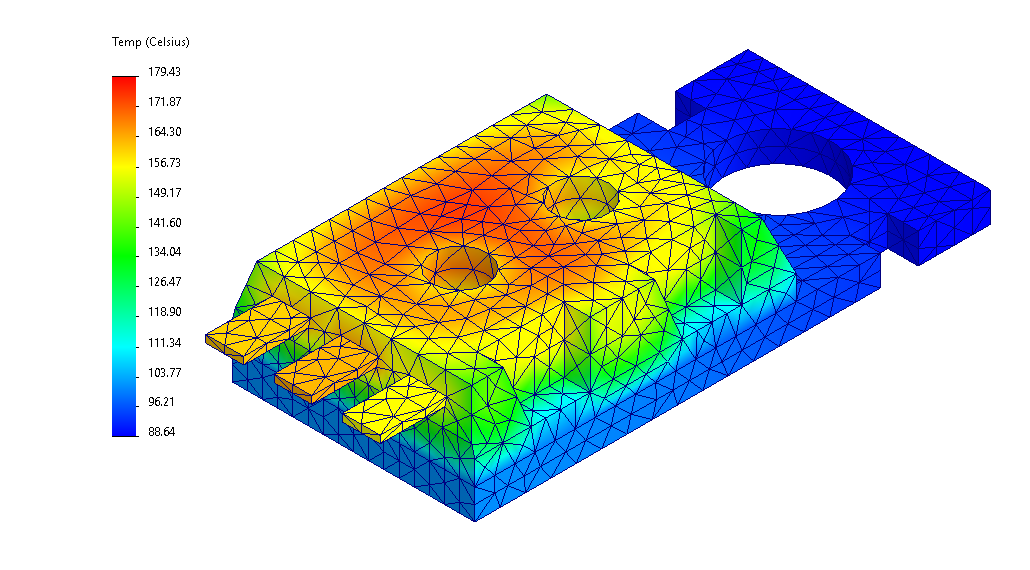 |
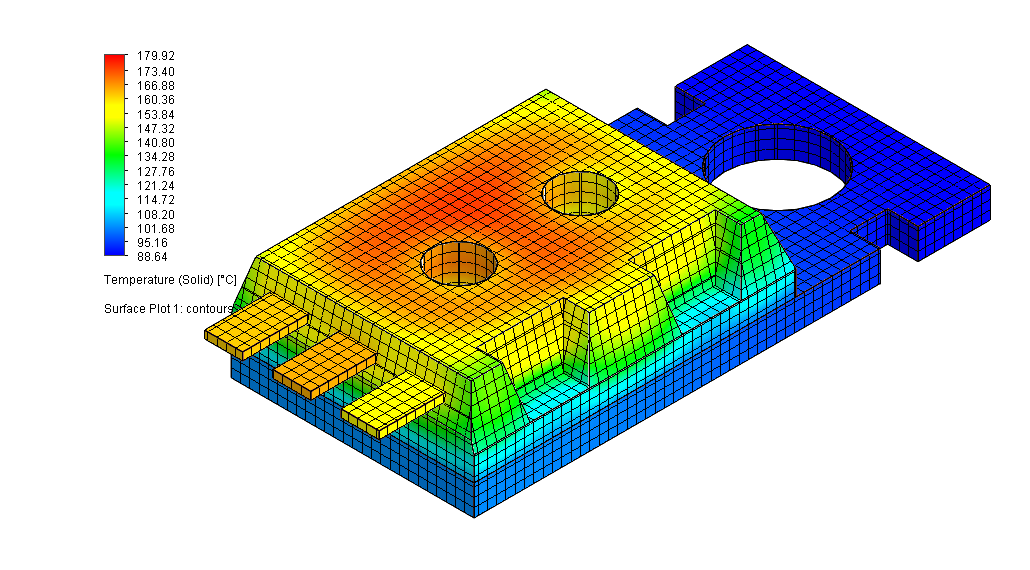 |
Rys. 9 Rozkład temperatury w złożeniu mikroprocesora w czasie t = 300 s obliczony z wykorzystaniem metody: FEM (lewo) oraz FVM (prawo).
Aby bardziej dokładnie porównać dwie metody obliczeniowe, wykonano wykres zmiany temperatury w wierzchołku na miedzianym złączu (Rys. 8 – zielony okrąg) w funkcji czasu. Zmiany temperatury w obydwu metodach przedstawiono na poniższym wykresie.
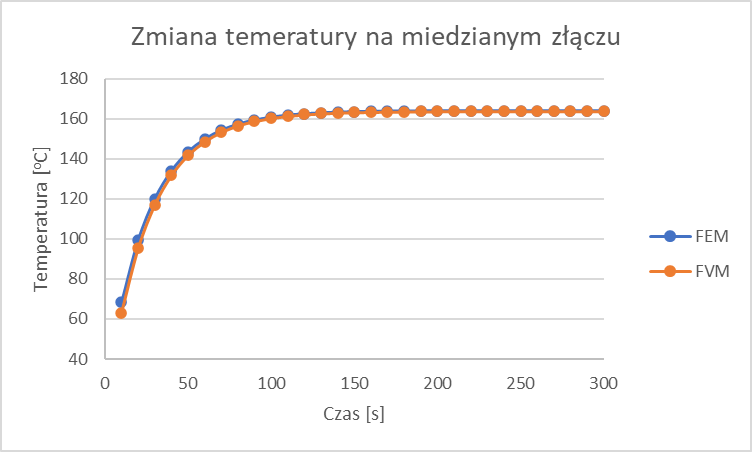
Rys. 10 Zmiana temperatury na miedzianym złączu w funkcji czasu.
Różnice w wyznaczonych temperaturach można zaobserwować w początkowym etapie symulacji, poniżej 100s. W przypadku metody FEM wyznaczone temperatury są nieznacznie wyższe niż w przypadku metody FVM, jednak ta różnica zanika dla większych czasów. Nie jest to konsekwencja różnic w metodzie obliczeniowej, a najprawdopodobniej przyczyną tej rozbieżności jest nieodpowiednia siatka zastosowana w metodzie FEM, co można było zobaczyć na Rys. 9. Aby to zweryfikować należałoby wykonać obliczenia dla drobniejszych siatek.
Analiza przypadku – przewodzenie, konwekcja i promieniowanie
W ostatnim przypadku przyjrzymy się procesowi wymiany ciepła, który łączy trzy mechanizmy: przewodzenie, konwekcję i promieniowanie. Przedstawimy go na przykładzie złożenia składającego się z aluminiowego reflektora, żarówki oraz szklanej pokrywy. Źródłem ciepła jest żarówka o mocy 50 W. Transport ciepła zachodzi na drodze przewodzenia w aluminiowej obudowie i szklanej pokrywie. Ze względu na brak płynu wewnątrz złożenia (próżnie), jednym z dominującym mechanizmów wymiany ciepła jest promieniowanie od powierzchni żarówki do ścian reflektora i szklanej pokrywy. Ostatni mechanizm, konwekcja, definiuje oddawanie ciepła na zewnątrz układu, z powierzchni aluminiowego reflektora i szklanej pokrywy. Schemat analizowanego układu zaprezentowano na poniższym rysunku.
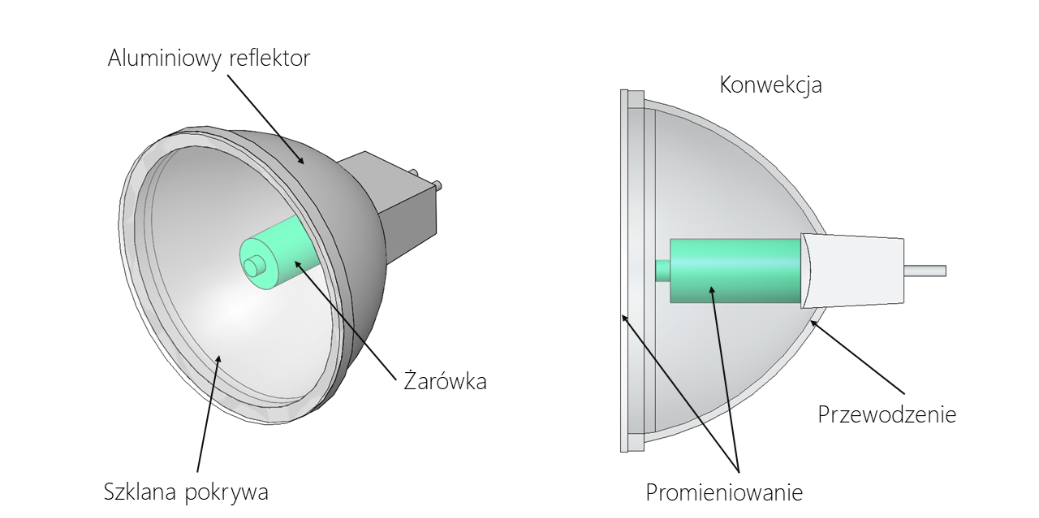
Rys. 11 Schemat analizowanego złożenia reflektora.
Ze względu na zastosowanie różnych materiałów, konieczne było nie tylko uwzględnienie różnych stałych materiałowych, ale również różnych współczynników emisji (promieniowanie) oraz współczynników wnikania ciepła (konwekcja). Wykorzystane wartości zestawiono w poniższej tabeli:
| Szklana żarówka | Szklana pokrywa | Aluminium | |
| Współczynnik przewodzenia ciepła [W/mK] | 0.74976 | 0.74976 | 160 |
| Pojemność cieplna [J/kgK] | 834.61 | 834.61 | 960 |
| Gęstość [kg/m3] | 2457.6 | 2457.6 | 2800 |
| Współczynnik emisji | 0.7 | 0.97 | – |
| Współczynnik wnikania ciepła [W/m2K] | – | 70 | 50 |
Wyniki obliczeń przedstawiono na Rys. 12. Aby pokazać wyniki wewnątrz złożenia, szklana pokrywa została ukryta na wykresach. W obydwu wypadkach, wyznaczone maksymalne temperatury są bardzo wysokie i wynoszą odpowiednio: 1002 oC (FEM) oraz 978 oC (FVM). Maksymalne wartości obserwowane są w objętości żarówki, podczas gdy w pozostałej części układu wartości temperatury nie przekraczają 300 oC. Jest to konsekwencja zbyt dużego uproszczenia układu. Żarówka nie powinna być modelowana jako źródło objętościowe ciepła w całej swojej objętości – tylko mała jej część (żarnik) powinna być źródłem ciepła i dodatkowo powinniśmy rozpatrywać promieniowanie od żarnika do zewnętrznych ścian żarówki. Jednak, aby przyśpieszyć proces analizy, przyjęto założenie, że cała objętość żarówki jest źródłem ciepła. Porównując otrzymane wyniki dla dwóch metod można zaobserwować różnice w rozkładzie temperatury w obrębie żarówki. Jednak ze względu na omówione wcześniej zbyt duże uproszczenie oraz różnice w siatce, nie będziemy się skupiać na tym elemencie symulacji.
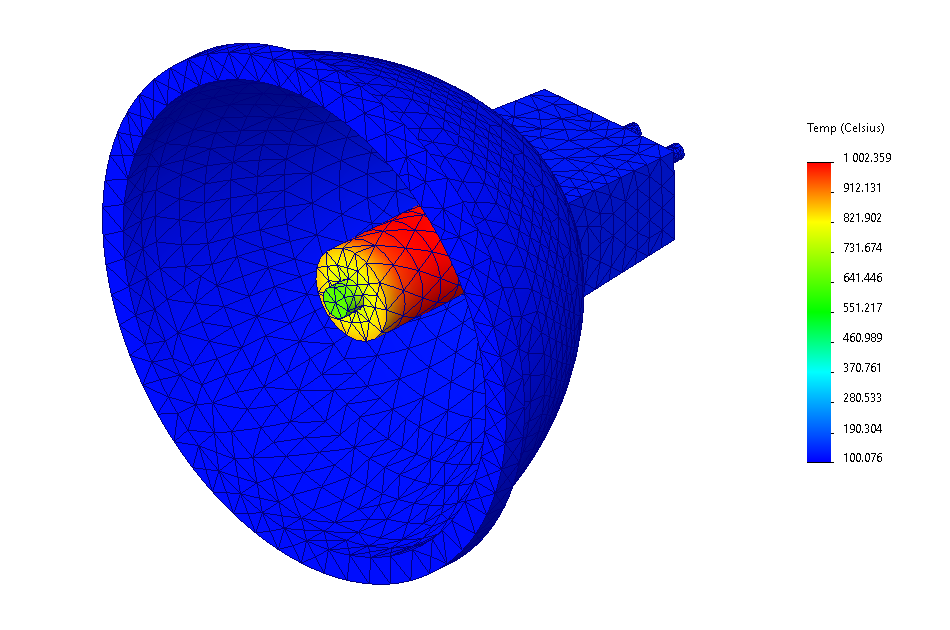 |
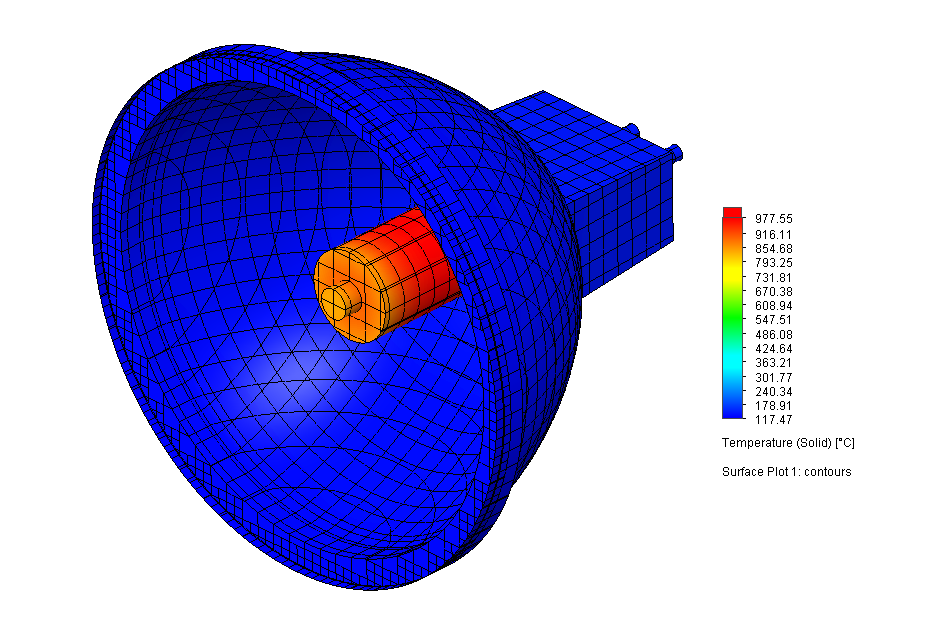 |
Rys. 12 Rozkład temperatury w złożeniu reflektora wyznaczony za pomocą: FEM (lewo) oraz FVM (prawo). Aby poprawić widoczność wyników, szklana pokrywa została ukryta na rysunkach.
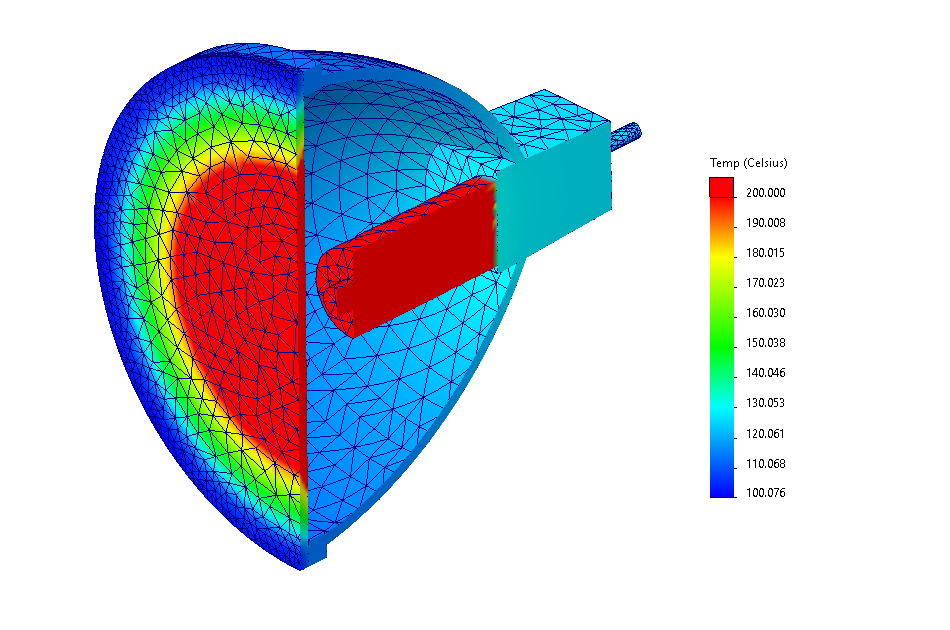
Aby lepiej zobrazować rozkład temperatury w układzie, zdecydowano się znormalizować maksymalne wartości temperatury na wykresie do 200 oC. Wyniki zawierające rozkład temperatury w obudowie, żarówce oraz szklanej pokrywce zaprezentowano na Rys. 13. Wykresy pokazują, że wyniki otrzymane dla metod FEM i FVM są identyczne. Maksymalne temperatury obserwowane są nie tylko w żarówce ale również w szklanej pokrywce, co pokazuje ze jest to główna powierzchnia, przez którą ciepło jest oddawane na zewnątrz układu.
 |
 |
Rys. 13 Znormalizowany rozkład temperatury w złożeniu reflektora wyznaczony za pomocą: FEM (lewo) oraz FVM (prawo). Wyniki pokazane są dla połowy układu.
Wiedząc, że otrzymane wyniki, z pominięciem rozkładu bardzo wysokich temperatur w żarówce, są zbliżone, pozostaje nam porównanie informacji o siatce i czasie obliczeń. Informacje te zestawiono w tabeli poniżej. Obliczenia wykonano dla siatek, które składały się z ok. 20 000 elementów (FEM) oraz ok. 18 000 komórek (FVM). Pomimo „zbliżonych” wartości elementów/komórek, różnice w czasie obliczeń są diametralne – 3 min 53 s dla FEM i 11 s dla FVM. Warto zaznaczyć, że analizowaliśmy proces w stanie stacjonarnym, więc znaczny przyrost czasu obliczeń nie wynika z analizy procesu ewolucyjnego, a z wprowadzenia promieniowania jako jednego z mechanizmów wymiany ciepła.
| FEM | FVM | |
| Liczba elementów | 20 382 | – |
| Liczba stopni swobody | 40 425 | – |
| Liczba komórek | – | 17 808 |
| Czas obliczeń | 3 min 53 s | 11 s |
Podsumowanie
Metody obliczeniowe, na których opierają się programy SOLIDWORKS Simulation (FEM) oraz SOLIDWORKS Flow Simulation (FVM) z powodzeniem mogą zostać wykorzystane do symulacji procesów wymiany ciepła. Na podstawie trzech zaprezentowanych przykładów mogliśmy zaobserwować że:
- w przypadku stacjonarnego procesu przewodzenia metoda FEM pozwala na szybsze uzyskanie wyników;
- w przypadku ewolucyjnego procesu przewodzenia i konwekcji metoda FVM pozwala na znacznie szybsze uzyskanie wyników. Przy analizie procesu stacjonarnego czas obliczeń dla obu metod jest zbliżony;
- w przypadku stacjonarnego procesu wymiany ciepła na drodze przewodzenia, konwekcji i promieniowania metoda FVM jest zdecydowanie szybsza niż metoda FEM.
Warto mieć na uwadze, że są to obserwacje na bazie trzech prostych przypadków, i wskazują tylko ogólną zależność. Należy podkreślić, że ze względu na fundamentalne różnice w zasadzie działania metod FEM i FVM, zastosowane siatki w obliczeniach nie mogą być w prosty sposób porównane. W konsekwencji otrzymane obliczenia nie możemy rozpatrywać jako konkretne informacje, a raczej jako wartości orientacyjne.
Drugim istotnym aspektem jest fakt, że zaprezentowane zagadnienia są tylko częścią z możliwych zastosowań analizy termicznej. W każdym z nich pominęliśmy fakt transportu ciepła w płynie, ponieważ takie obliczenia nie są możliwe z wykorzystaniem metody FEM zaimplementowanej w programie SOLIDWOKKS Simulation. Powoduje to, że procesy w których konwekcja miałaby zachodzić na drodze konwekcji swobodnej, a nie wymuszonej (gdzie znamy współczynniki wnikania ciepła), nie są możliwe.
Mam nadzieję, że zapoznanie się z tym artykułem wyjaśniło ogólne różnice między FEA (FEM) i CFD (FVM) oraz ich zastosowanie w symulacjach procesów transportu ciepła. Warto zaznaczyć, że obie metody mogą zostać efektywnie wykorzystane do analizy wielu zagadnień, choć dla niektórych procesów wybór jednej z nich może pozwolić uzyskać wyniki szybciej. Zapraszam do zapoznania się z innymi naszymi publikacjami w zakresie projektowania, symulacji, zarządzania i wytwarzania oraz życzę powodzenia w symulacjach!