Szkice konstrukcyjne
Zbudowanie koła zębatego wymaga znajomości podstaw ich geometrii. Poniżej przedstawiono podstawowe wymiary niezbędne do zaprojektowania koła zębatego.
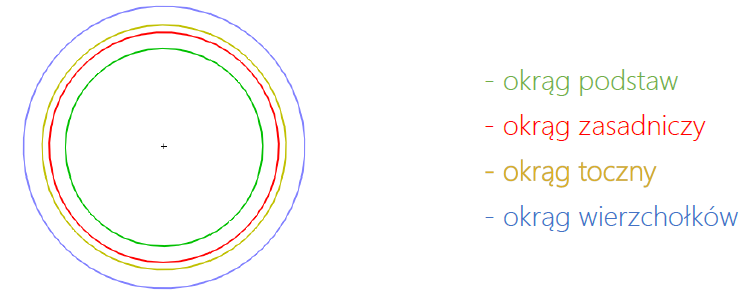
Wartości średnic należy odczytać z odpowiednich normatyw.
Zarys ewolwentowy
Funkcja ewolwentowa wyraża się w poniższych zależnościach:
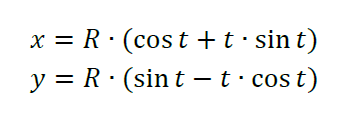
gdzie R jest promieniem okręgu zasadniczego.
Parametr ten należy zdefiniowany jako Zmienna globalna powołując się na wymiar średnicy okręgu zasadniczego.
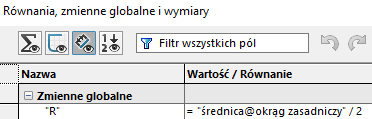
Wyrażenie na ewolwentę zaimplementować można dzięki Krzywej opartej na równaniu.

Definiujemy równania parametryczne, w których powołujemy się na zmienną globalną R.
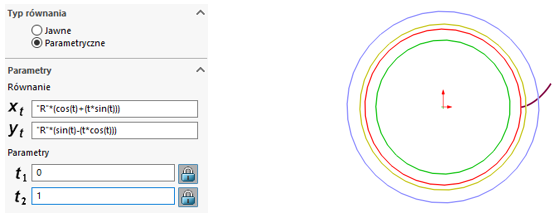
Ewolwenta rozwijana jest z okręgu zasadniczego.
Kolejne etapy rysowania kształtu zęba
Szerokość zęba S definiujemy po okręgu tocznym.
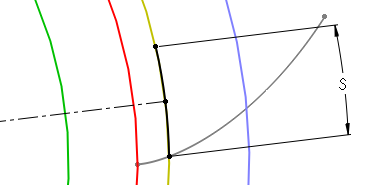
Łącząc środek łuku szerokości ze środkiem koła wyznaczamy linię symetrii zęba; tym samym mamy możliwość odbicia lustrzanego jednej strony zarysu zęba.
Uzyskujemy ewolwentowe zarysy obu stron zęba.
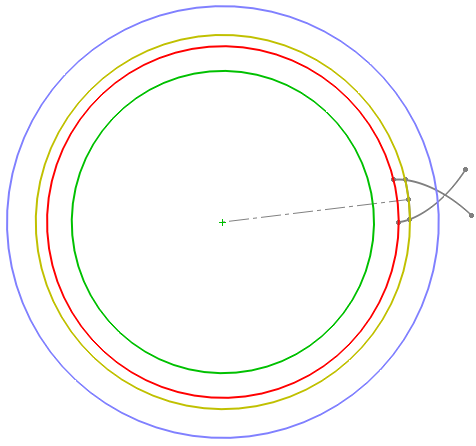
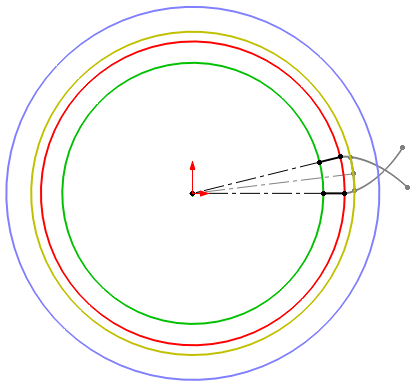
Rysujemy stopy zęba łącząc liniami promieniowymi podstawy ewolwenty z okręgiem podstaw.
Jest to jednocześnie linia promieniowa między okręgiem podstaw a okręgiem zasadniczym.
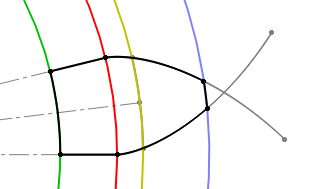
Kształt zęba wyznaczają: zarysy ewolwentowe, promieniowe odcinki stopy, okrąg podstaw i okrąg wierzchołków.
Linia przyporu
SOLIDWORKS pozwala wykreślić schemat, który posłużyć może do analizy warunków współpracy uzębień.
Linia przyporu prowadzona jest przez kolejne Punkty przyporu, czyli miejsca zetknięcia zębów.
Kąt przyporu α mierzony jest między linią przyporu a styczną do okręgów tocznych.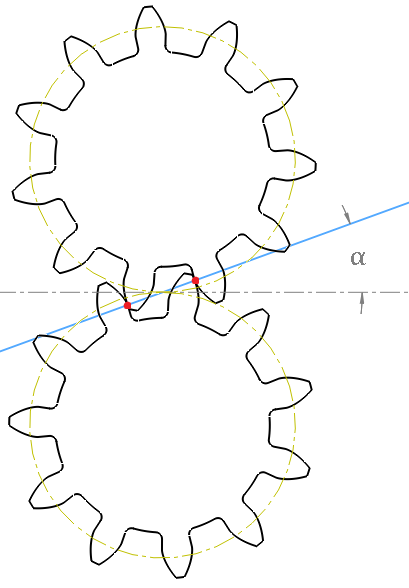
Zalety
Główną cechą współpracy kół zębatych o zarysie ewolwentowym jest zachowanie stałego kierunku siły międzyzębnej w czasie pracy.

