Tarcie, zjawisko tak często pomijane, niezwykle istotne w symulacjach procesów technologicznych czy analizach wytrzymałościowych. W artykule przedstawiono wpływ tarcia na geometrię i pole odkształcenia próbki cylindrycznej poddanej osiowemu ściskaniu.
Schemat badania
Próbkę cylindryczną o średnicy d0=10 mm i wysokości h0=1.5‣d0 poddano spęczaniu (ściskaniu) o 50%. Zastosowano plastyczny model materiału próbki o charakterystyce zobrazowanej na wykresie σ-Ɛ (rys. 1). Kowadła ustawiono jako obiekty niedeformowalne.
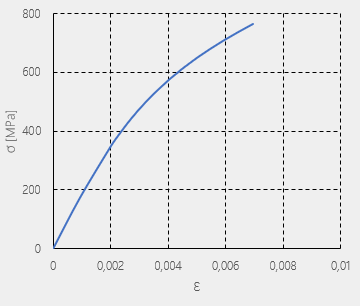 |
| Rys. 1. Krzywa rozciągania |
Z uwagi na osiowosymetryczny charakter zjawiska doświadczenia, zastosowano uproszczenie planarne co w znaczący sposób zredukowało czas symulacji.
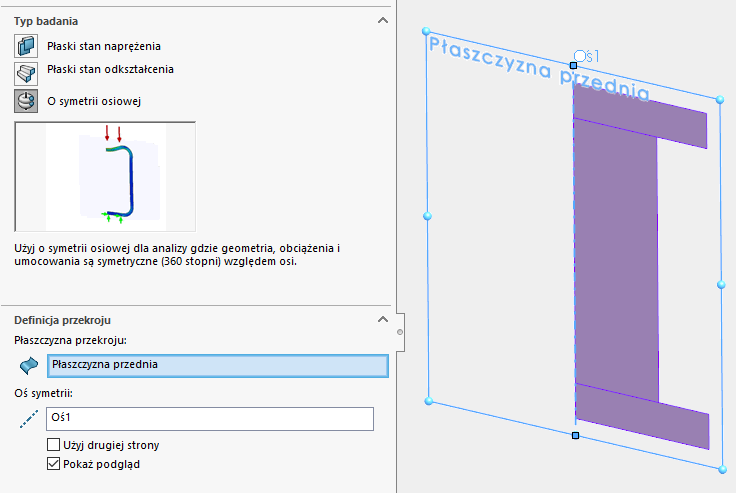 |
| Rys. 2. Planarne uproszczenie (osiowosymetryczne) statycznej analizy nieliniowej |
Zestawy kontaktowe Bez penetracji definiowane pomiędzy próbką a kowadłami pozwoliły odwzorować realistyczne oddziaływanie pomiędzy nimi (rys. 3).
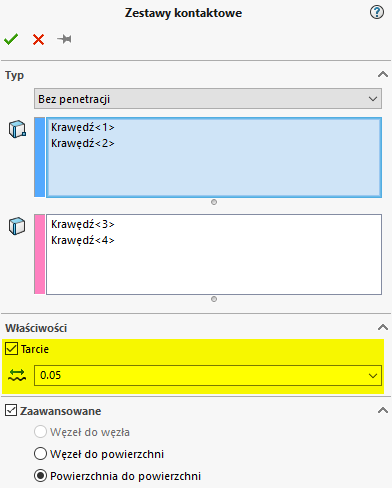 |
| Rys. 3. Definicja zestawu kontaktowego bez penetracji z uwzględnieniem tarcia |
W artykule przeprowadzono symulacje z kontaktem bez tarcia, oraz dla współczynnika o wartości 0.05 i 0.2.
Wyniki
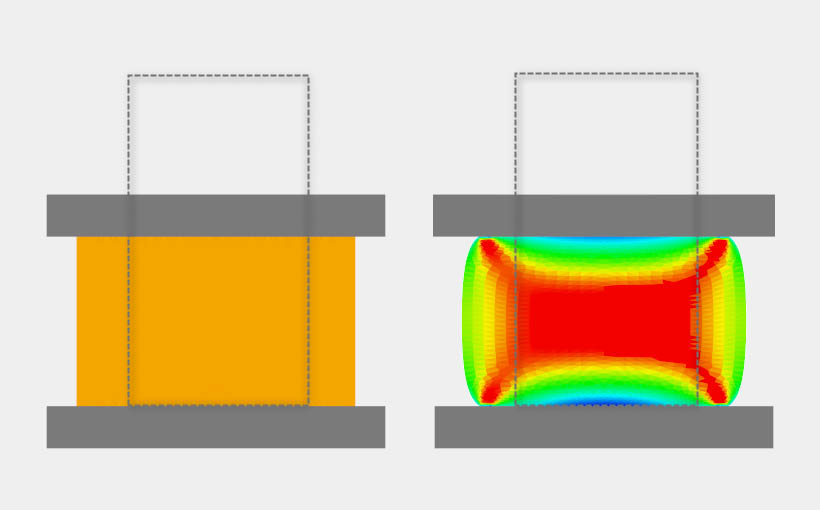
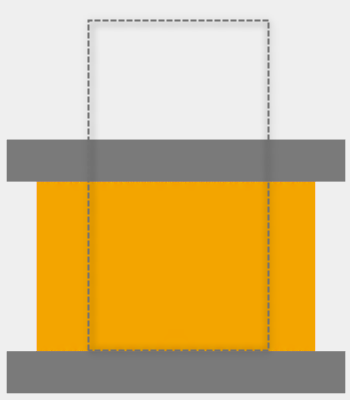
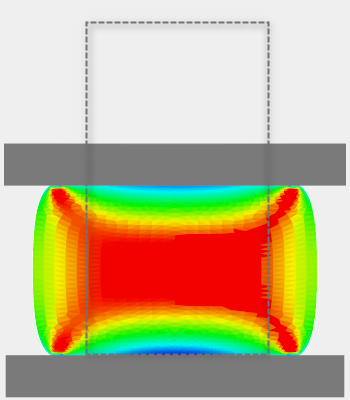
Rysunek 4 przedstawia pole odkształcenia w próbce spęczanej bez tarcia oraz dla współczynnika 0.2. Przerywane linie obrazują kształt próbki przed deformacją.
| a)
|
b)
|
 |
| Rys. 4. Pole rozkładu odkształcenia w procesie bez tarcia (a) oraz z tarciem (b) | ||
Przy spęczaniu z uwzględnieniem tarcia materiał płynie w charakterystyczny sposób – ujawnia się beczkowaty kształt próbki po spęczaniu. Gdy tarcie jest pominięte ściany pobocznicy pod deformacji dalej pozostają pionowe.
Poniższy wykres przedstawia krzywą zależności zmiany promienia Δr od współczynnika tarcia μ, gdzie r mierzono w najszerszym punkcie próbki (rys. 5).
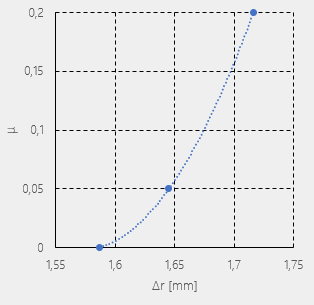 |
| Rys. 5. Zależność przyrostu promienia Δr od zastosowanego współczynnika tarcia μ |
Charakterystyka wyznaczona w oparciu o trzy punkty pozwoliła na wykreślenie wielomianowej zależności.
Podsumowanie
Zjawisko tarcia stanowi jeden z głównych mechanizmów rozproszenia energii na granicy dwóch współpracujących ze sobą ciał. Warunkuje charakter płynięcia materiału w procesach plastycznej przeróbki, przez co ma istotny wpływ na kształt finalnego produktu.